Request a Tool
Stokes Law Calculator
Stokes Law Calculator is useful in calculating various parameters of fluid in viscometer.
Input
Output
Formula
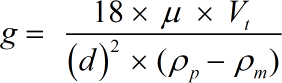
- g = Acceleration of Gravity
- d = Particle Diameter
- Pm = Density of Medium
- Pp = Particle Density
- μ = Viscosity of Medium
- Vt = Fall or Settling Velocity
Defination / Uses
Stoke's law states that at low velocities the frictional force on a spherical body moving through a fluid at constant velocity is equal to 6 π times the product of the velocity, the fluid viscosity, and the radius of the sphere.
In short, a sphere moving through a viscous fluid is directly proportional to the velocity of the sphere as well as the radius of the sphere, and the viscosity of the fluid. Stoke's Law is defined as the basis of the falling - sphere viscometer. In the viscometer the fluid is stationary in a vertical glass tube
Input
Output
Formula
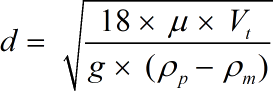
- d = Particle Diameter
- Pm = Density of Medium
- Pp = Particle Density
- μ = Viscosity of Medium
- Vt = Fall or Settling Velocity
- g = Acceleration of Gravity
Defination / Uses
Stoke's law states that at low velocities the frictional force on a spherical body moving through a fluid at constant velocity is equal to 6 π times the product of the velocity, the fluid viscosity, and the radius of the sphere.
In short, a sphere moving through a viscous fluid is directly proportional to the velocity of the sphere as well as the radius of the sphere, and the viscosity of the fluid. Stoke's Law is defined as the basis of the falling - sphere viscometer. In the viscometer the fluid is stationary in a vertical glass tube
Input
Output
Formula
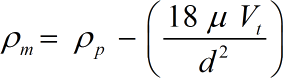
- Pm = Density of Medium
- Pp = Particle Density
- μ = Viscosity of Medium
- Vt = Fall or Settling Velocity
- g = Acceleration of Gravity
- d = Particle Diameter
Defination / Uses
Stoke's law states that at low velocities the frictional force on a spherical body moving through a fluid at constant velocity is equal to 6 π times the product of the velocity, the fluid viscosity, and the radius of the sphere.
In short, a sphere moving through a viscous fluid is directly proportional to the velocity of the sphere as well as the radius of the sphere, and the viscosity of the fluid. Stoke's Law is defined as the basis of the falling - sphere viscometer. In the viscometer the fluid is stationary in a vertical glass tube
Input
Output
Formula
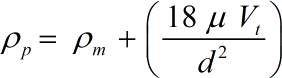
- Pp = Particle Density
- μ = Viscosity of Medium
- Vt = Fall or Settling Velocity
- g = Acceleration of Gravity
- d = Particle Diameter
- Pm = Density of Medium
Defination / Uses
Stoke's law states that at low velocities the frictional force on a spherical body moving through a fluid at constant velocity is equal to 6 π times the product of the velocity, the fluid viscosity, and the radius of the sphere.
In short, a sphere moving through a viscous fluid is directly proportional to the velocity of the sphere as well as the radius of the sphere, and the viscosity of the fluid. Stoke's Law is defined as the basis of the falling - sphere viscometer. In the viscometer the fluid is stationary in a vertical glass tube
Input
Output
Formula
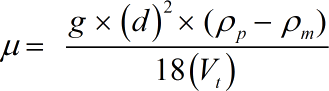
- μ = Viscosity of Medium
- Vt = Fall or Settling Velocity
- g = Acceleration of Gravity
- d = Particle Diameter
- Pm = Density of Medium
- Pp = Particle Density
Defination / Uses
Stoke's law states that at low velocities the frictional force on a spherical body moving through a fluid at constant velocity is equal to 6 π times the product of the velocity, the fluid viscosity, and the radius of the sphere.
In short, a sphere moving through a viscous fluid is directly proportional to the velocity of the sphere as well as the radius of the sphere, and the viscosity of the fluid. Stoke's Law is defined as the basis of the falling - sphere viscometer. In the viscometer the fluid is stationary in a vertical glass tube
Input
Output
Formula
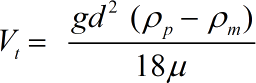
- Vt = Fall or Settling Velocity
- g = Acceleration of Gravity
- d = Particle Diameter
- Pm = Density of Medium
- Pp = Particle Density
- μ = Viscosity of Medium
Defination / Uses
Stoke's law states that at low velocities the frictional force on a spherical body moving through a fluid at constant velocity is equal to 6 π times the product of the velocity, the fluid viscosity, and the radius of the sphere.
In short, a sphere moving through a viscous fluid is directly proportional to the velocity of the sphere as well as the radius of the sphere, and the viscosity of the fluid. Stoke's Law is defined as the basis of the falling - sphere viscometer. In the viscometer the fluid is stationary in a vertical glass tube
How to use Stoke's law calcultor?
There are only two basic steps.
- First select the option from dropdown. What you need to calculate.
- Then add values other than requirement in their corresponding fields.
Thats it! You will get your answer in less than a single second.
The Stokes Law Calculator is an online tool that calculates the terminal velocity in a fraction of a second after entering the inputs viscosity, fluid density, and particle density and diameter. Using the helpful calculator, make your calculations simple and acquire the object's final velocity quickly. No sign-up, registration OR captcha is required to use this tool.