Request a Tool
Complex Number Calculator
Complex Number Calculator use to calculate multiplication, division and square root of complex numbers.
Input
Output
Formula
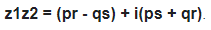
- z1z2 = Multiplication of Two Complex number
- p = Value of 1a
- q = Value of 1bi
- r = Value of 2a
- s = Value of 2bi
Defination / Uses
To put it another way, you simply multiply the real number by both parts of the complex number. 2 times 3 + I for example, equals 6 + 2i. When you double a complex number geometrically, you simply double the distance from the origin, which is 0.
Input
Output
Formula
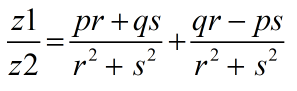
- z1/z2 = Division of Two Complex number
- p = Value of 1a
- q = Value of 1bi
- r = Value of 2a
- s = Value of 2bi
Defination / Uses
Multiplying the numerator and denominator by the complex conjugate of the denominator, for example, with and, yields the division of two complex numbers. (1) and (2) (3)
Input
Output
Formula
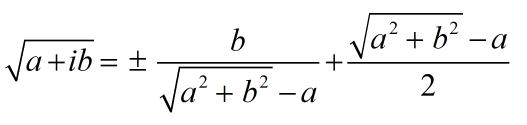
- a = Value of a
- b = Value of bi
Defination / Uses
By definition of a square root, all square roots of this number will meet the equation 21-20i=x2. We also know that x can be written as a+bi (where a and b are real) since complex numbers' square roots are always complex. As a result, 21-20i=(a+bi)2
Our complex number calculator (also known as an imaginary number calculator) is a useful tool for performing simple complex number operations. Continue reading to learn the answer to the question "what is a complex number?" as well as the algebraic and polar forms of complex numbers and how to multiply and divide them. You can also discover information about complex numbers' properties (most of which are based on the conjugate or absolute value of complex numbers) and some practical applications near the end of this text.