Request a Tool
Reynolds Number Calculator: Quick and Accurate Fluid Flow Tool
Reynolds Number Calculator tool is easy to use and displays the Reynolds number, which is used to assess whether a fluid is laminar or turbulent.
Input
Output
Formula
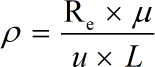
- ρ = refers to the density
- L = characteristic length
- u = velocity
- μ = dynamic viscosity
- v = μ / ρ = kinematic viscosity2
- Re = represents Reynolds Number
Input
Output
Formula
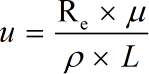
- u = velocity
- ρ = refers to the density
- L = characteristic length
- μ = dynamic viscosity
- v = μ / ρ = kinematic viscosity
- Re = represents Reynolds Number
Input
Output
Formula
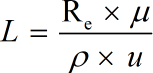
- L = characteristic length
- u = velocity
- ρ = refers to the density
- μ = dynamic viscosity
- v = μ / ρ = kinematic viscosity
- Re = represents Reynolds Number
Input
Output
Formula
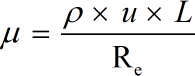
- μ = dynamic viscosity
- L = characteristic length
- u = velocity
- ρ = refers to the density
- v = μ / ρ = kinematic viscosity
- Re = represents Reynolds Number
Input
Output
Formula
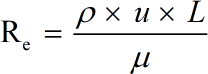
- Re = represents Reynolds Number
- μ = dynamic viscosity
- L = characteristic length
- u = velocity
- ρ = refers to the density
- v = μ / ρ = kinematic viscosity
What is Reynolds Number?
The Reynolds number is a ratio that supports the prediction of flow patterns in various fluid flow situations. Flows with high Reynolds numbers tend to be turbulent, and flows with low Reynolds numbers tend to be laminar. Because Reynolds number is a dimensionless parameter, there are no units for it. In other words, the Reynolds number is a quantity that is one unit less.
The flow of a fluid in parallel layers is referred to as laminar flow. Fluid flows in a laminar flow without being disrupted. Turbulent flow, on the other hand, refers to fluid that does not flow in parallel layers due to changes in velocity, pressure, and other factors. It flows across the tube in a layered pattern.
What is the Reynolds Number Calculator?
The Reynolds Number Calculator is a short-cut tool which will enable you to easily determine the Reynolds number-a versatile dimensionless quantity. The Reynolds number explains the nature of flow of a particular fluid whether it is smooth ordered or laminar, or random disordered or turbulent. The value of Reynolds number assists engineers and scientist most importantly in fluid mechanics, to predict the behavior of flowing fluids in those systems where fluid dynamics take a major part like pipe flow, airflow, river flow or any machine components.This calculator makes it easy to obtain accurate results by entering basic flow parameters, simplifying complex calculations for efficient analysis.
Why Use the Reynolds Number Calculator Tool
Saves Time and Effort
The calculator gives out the Reynolds number results immediately, sparing one the time that would be taken when doing the computations manually.
Reduces Calculation Errors
Reduces the amount of detailed computation and formulation generally involved to calculate flow characteristics.
Easy to Use
Requires only basic input on fluid properties and conditions, making it accessible for both students and professionals.
Ideal for Quick Assessments
Perfect for users needing fast and accurate results, helping avoid time-consuming math.
Informs Better Decisions
By understanding Reynolds number values, you can make smarter choices in fluid system design, troubleshooting, and optimization.
Where Can the Reynolds Number Calculator Tool Be Used
Engineering
Essential in designing fluid systems, such as HVAC systems, water pipelines, and chemical reactors.
Pipeline and Water Systems
To evaluate the flow type in pipes and water distribution systems, aiding in design and efficiency.
Automotive and Aerospace
Fuels aerodynamics and flow analysis of air over surfaces on which it passes over to predict the efficiency of its operation.
Medical and Biological Research
Medically, it’s well suited for the analyses of blood circulation and other body fluids, etc.
Automotive Design
To analyze coolant flows, fuel systems, and aerodynamic performance in vehicle engineering.
Agricultural Irrigation Systems
To determine flow patterns in irrigation channels and piping systems for optimal water distribution.
How to Use the Reynolds Number Calculator Tool
Using the Reynolds Number Calculator is simple and interactive:
1.Select Calculation Type
Choose the desired option from the dropdown menu. Based on your selection, relevant input fields will appear for you to enter the required parameters.
2.Enter Input Parameters
Enter all other parameters related to the fluid like velocity, viscosity, density, etc., as well as characteristic linear dimension like diameter of the pipe or tube.
3.Automatic Calculation
Once you have input the values, this tool automatically calculates the Reynolds number will be done and displayed in the output box.
4.Interpret Results
An analysis of the calculated Reynolds number will tell whether the flow is in the laminar, transitional or turbulent region. This shows that lower values will indicate laminar flow while higher values will indicate turbulent flow.
5.Clear Button
This button that allows you to clear the input fields and start a new calculation. This button is helpful when you need to perform multiple calculations or make changes to the input values.
Conclusion
The Reynolds Number Calculator can be used by any person interested in fluid dynamics ranging from high school learners to engineers. By simplifying complex calculations, it offers an accurate and efficient way to determine fluid flow patterns. This tool saves time and effort, making it a reliable resource for quickly assessing flow characteristics in various applications.
With just a few inputs, users can gain insights into whether a flow is laminar, transitional, or turbulent, helping them make informed decisions in the design, analysis, and optimization of fluid systems. This straightforward tool supports a wide range of fluid-related projects, enhancing understanding and decision-making in both educational and professional settings.