Request a Tool
Bernoulli Numbers Calculator
This tools is used to calculate the equivalent bernoulli value B(n) for the given numeric value which is used for mathematical analysis.
Input
Output
Formula
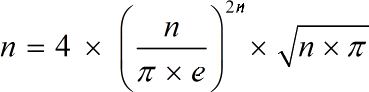
- n = large number
- e = constant value ( 2.718281828459...)
Defination / Uses
Bernoulli Numbers are the numbers that appear in the series expansions of trigonometric functions and are very essential in number theory and analysis. The Bernoulli Numbers are written in both modern and classic literature styles. Bernoulli Numbers in present usage are denoted by the symbol Bn, but those in older literature are marked by the symbol B(n).
How bernoulli numbers calculator work?
Its a single step procedure.
- Add the required value in its given field.
Thats it! You will get your answer in less than a second. Use upper given formula in case of manual calculation.
The Bernoulli numbers were discovered around the same time by Swiss mathematician Jacob Bernoulli, after whom they are named, and by Japanese mathematician Seki Takakazu, who found them independently. Seki's discovery was published posthumously in his work Katsuy Sanp in 1712, and Bernoulli's in his Ars Conjectandi in 1713. An algorithm for producing Bernoulli numbers with Babbage's machine is described in Ada Lovelace's note G on the Analytical Engine dated 1842. As a result, the Bernoulli numbers hold the distinction of being the first sophisticated computer programme to be published. For quick calculation use our weetools. No sign-up, registration OR captcha is required to use this tool.